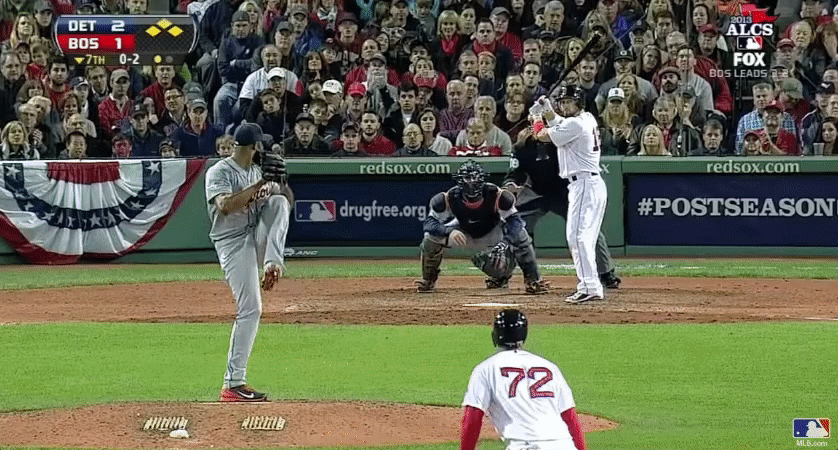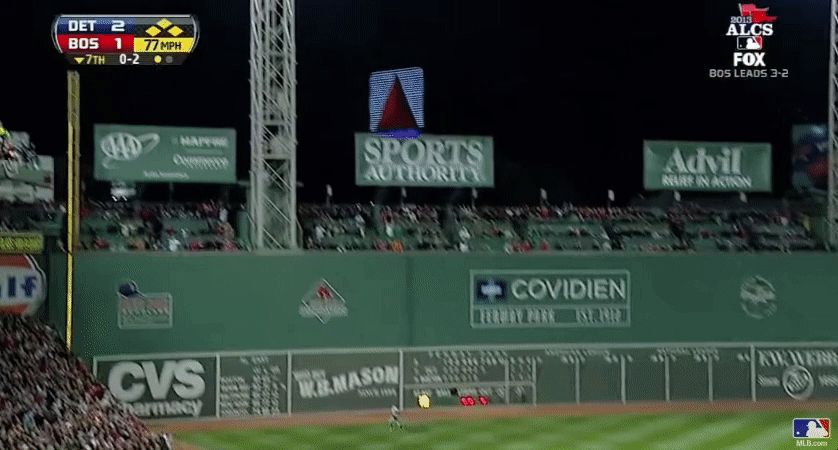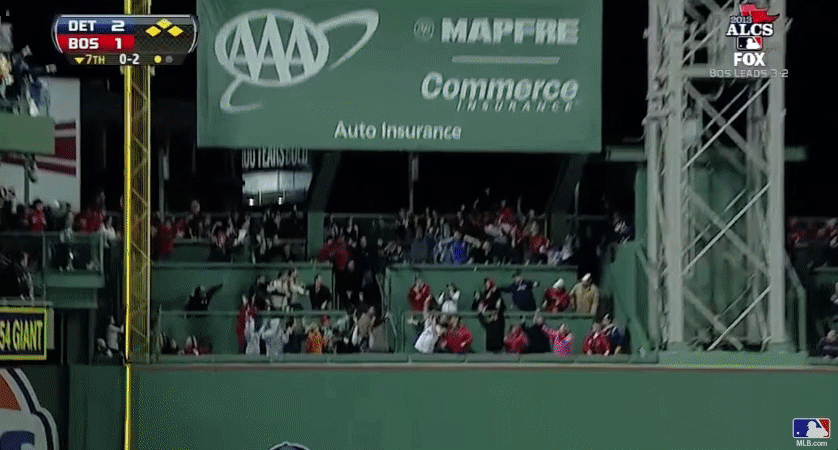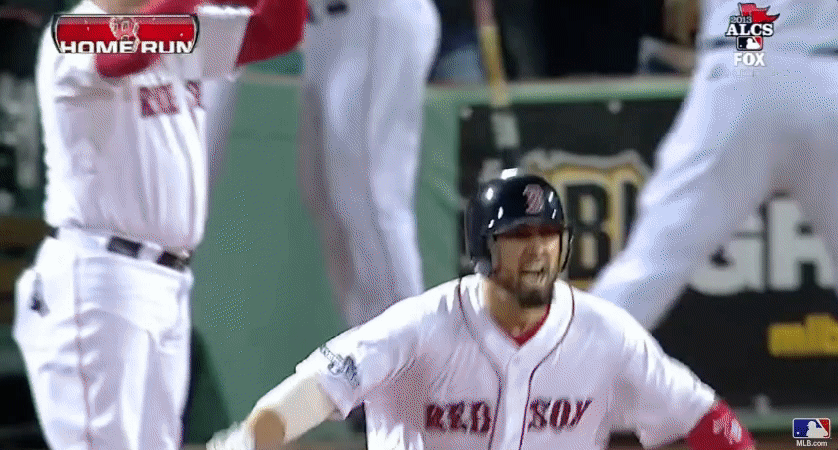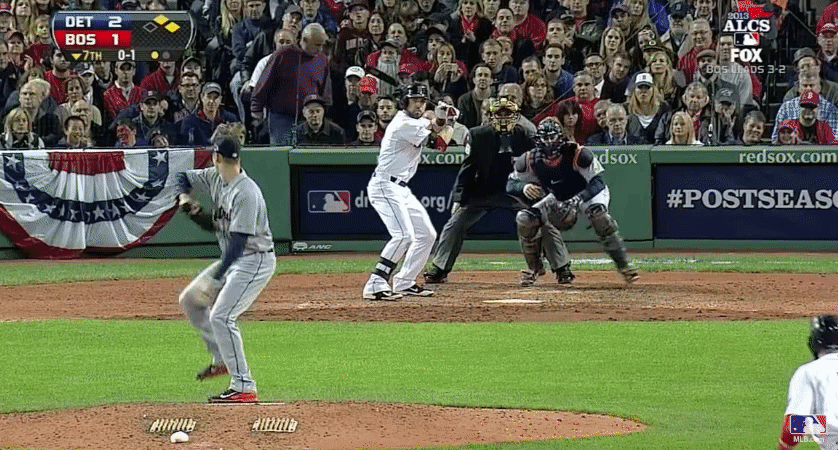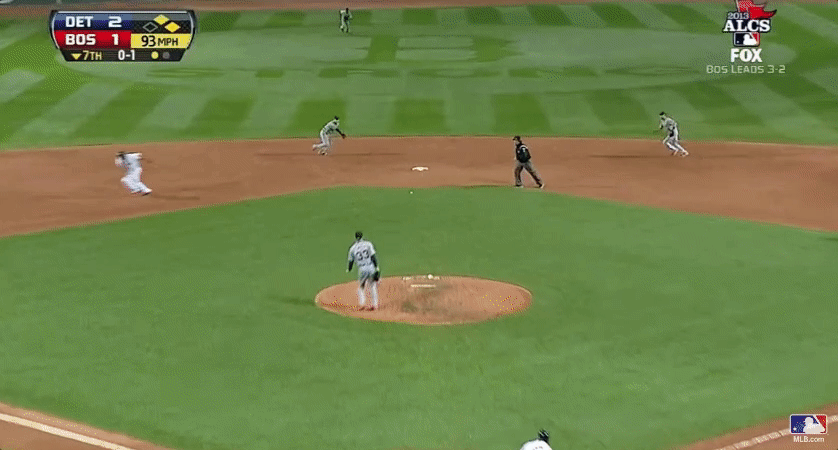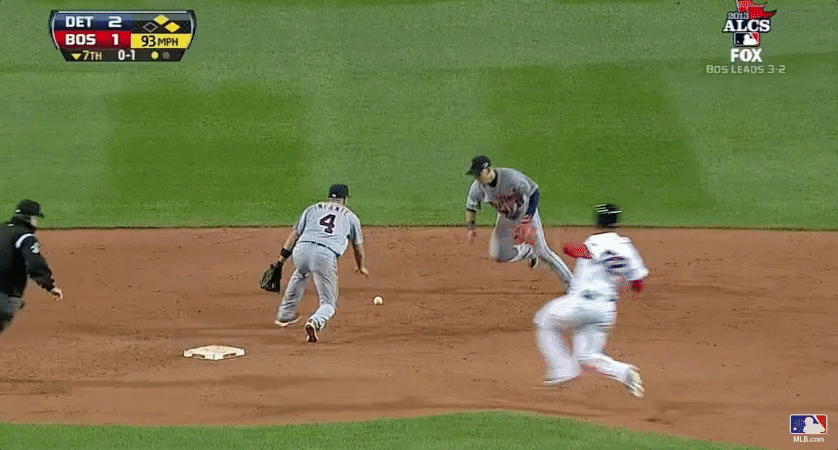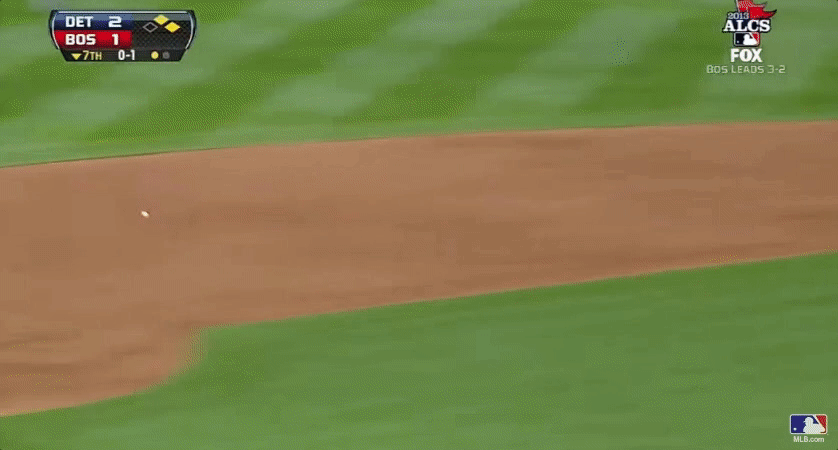What we remember
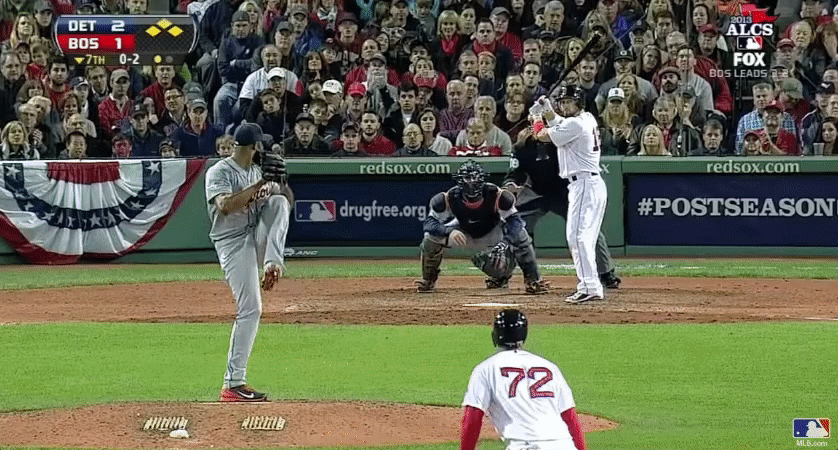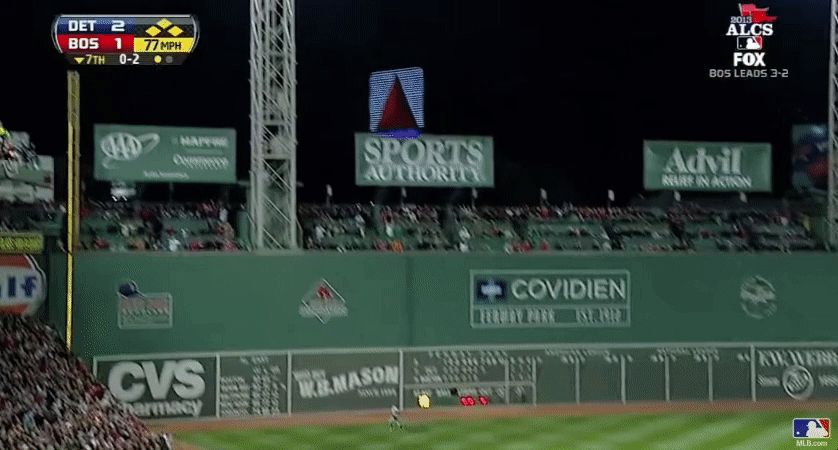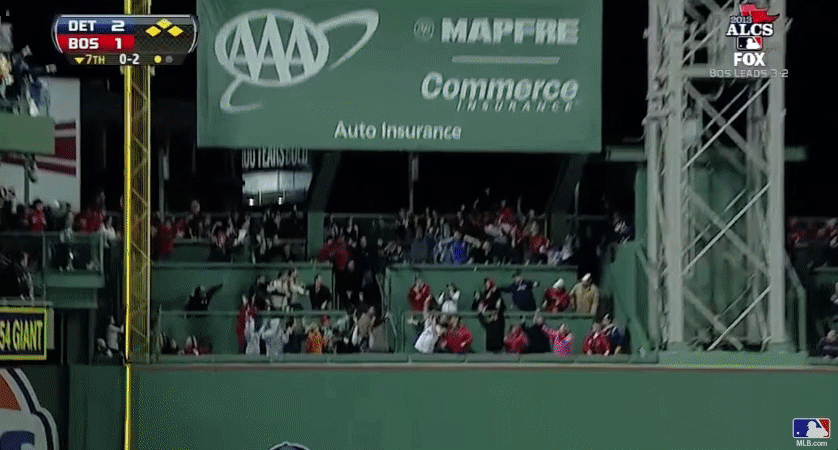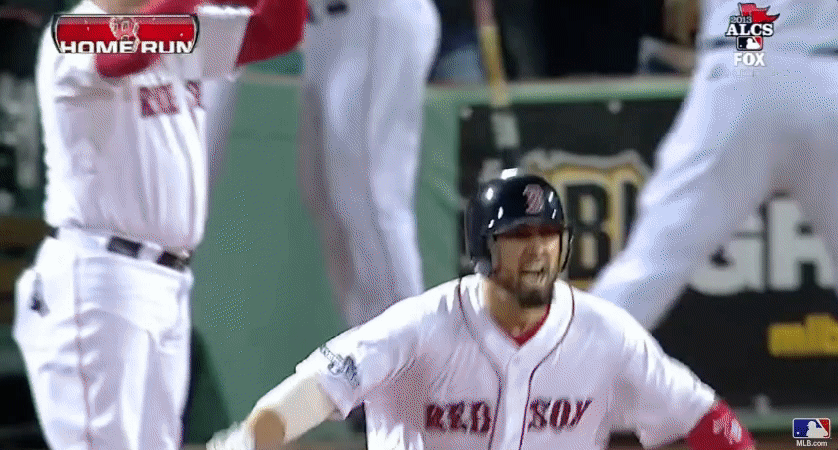
What we forget

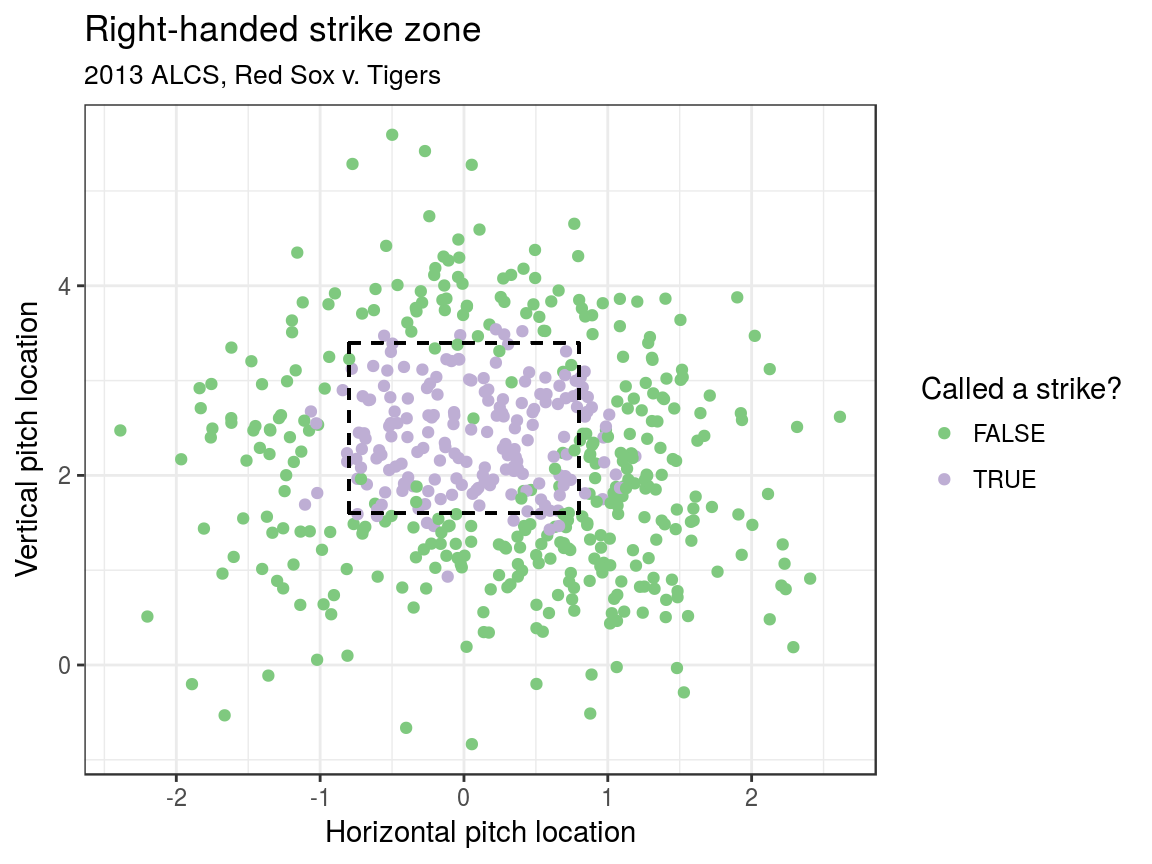
Pitches in the series
That pitch
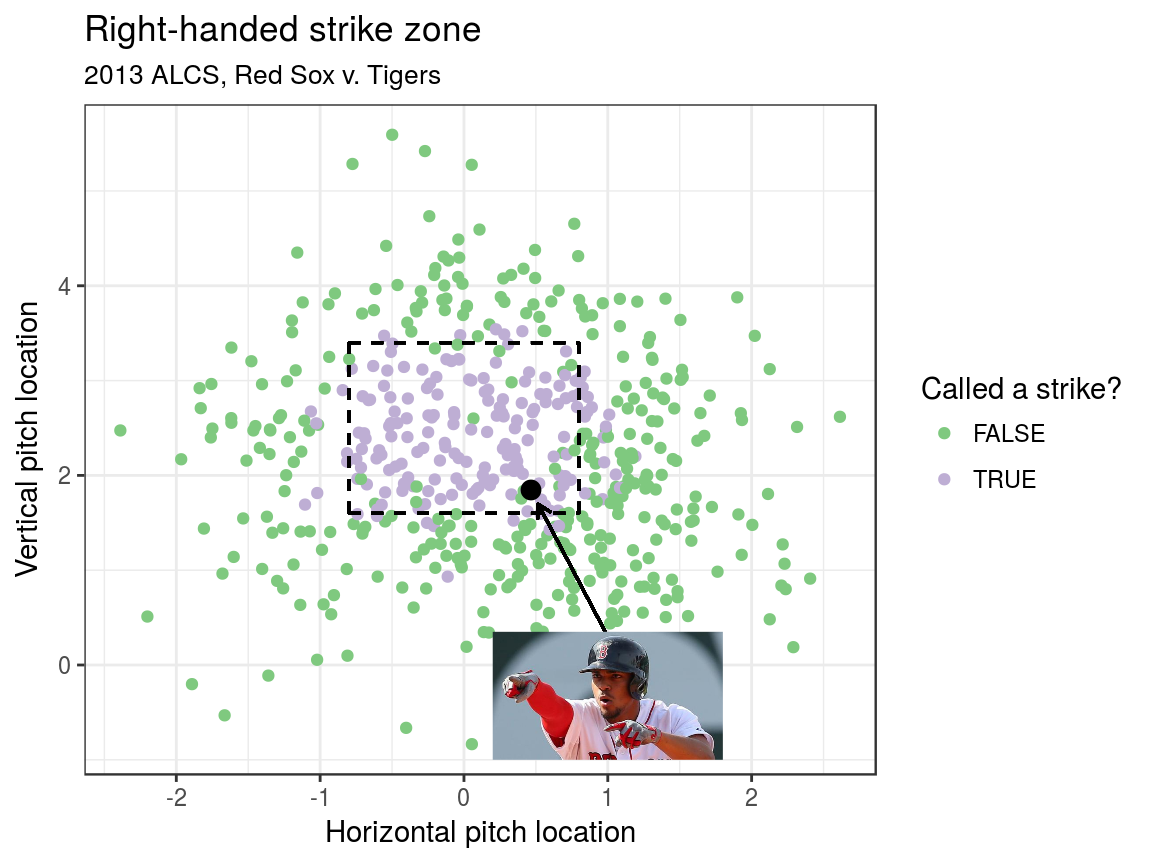
The truth is…
- About 80% of pitches taken at this location called a strike (using advanced modeling)
- Walk worth about 12% in win expectency (32% to 44%)
- Red Sox were lucky!
What we also forget
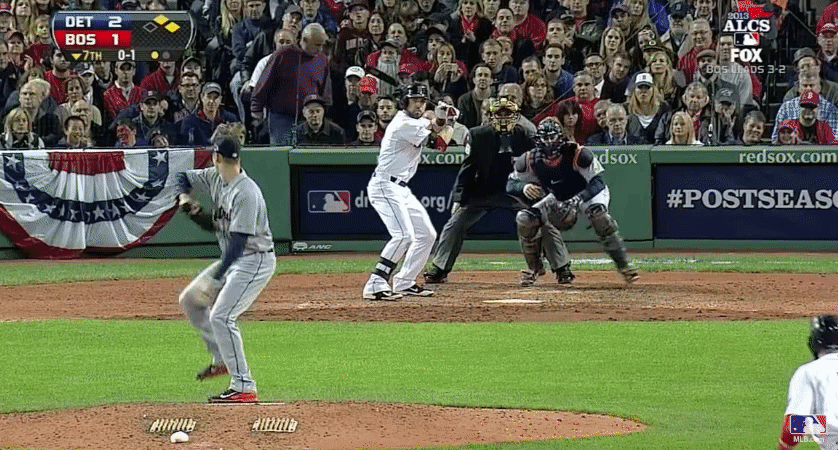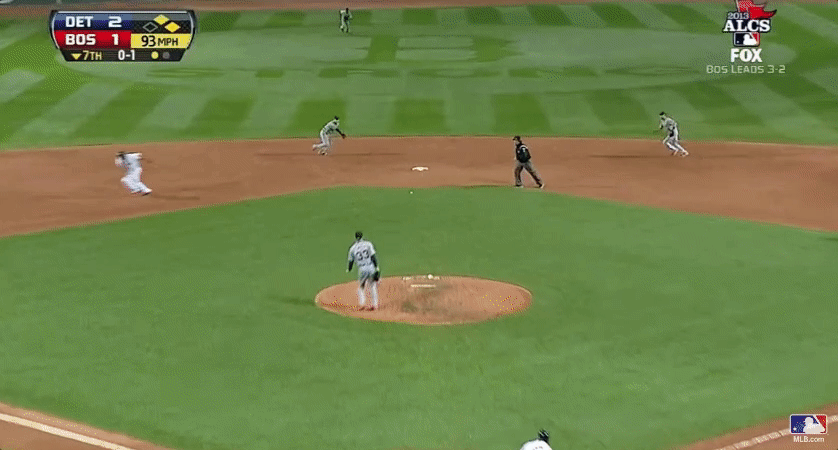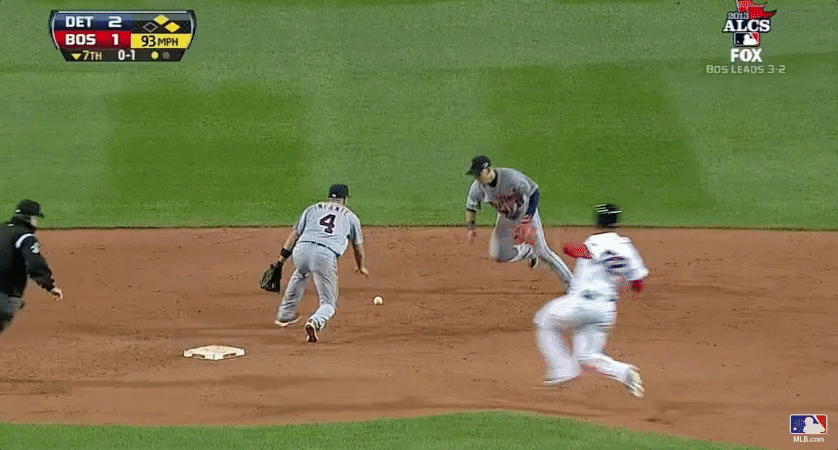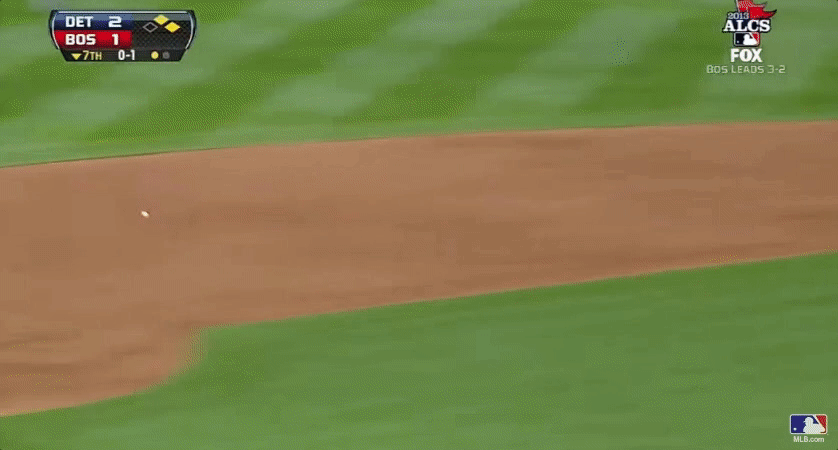
About that error…
- Jose Iglesias: 98.5% fielding percentage (Note: Statcast data unavailable)
- Error worth about 20% in win expectency over out at second (36% to 56%)
- Red Sox were lucky!
Summary
- Two huge swings in win probability that were outside the Red Sox control
- Red Sox were lucky!
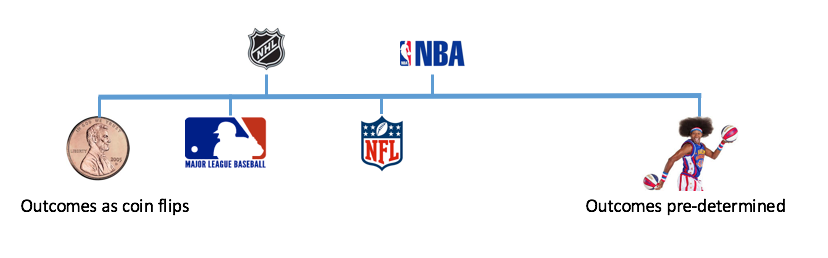
Using statistics to assess luck in sports
- The best team does not always win. (Sorry, Detroit)
- How to untangle luck from skill?
- How often does the best team win in each sport?
How to define parity
the state or condition of being equal
Google
What parity looks like

What parity does not look like

Parity checklist
- Equality at a fixed time
- Within season equality
- Between season equality
Prior work

Challenges
- Problem 1: wins and losses alone insufficient (noisy)
- Problem 2: point differential non-generalizable
- Solution: if you can’t beat ’em, use their numbers in a statistical model

Moneylines
 |
-127 |
0.559 |
0.548 |
 |
+117 |
0.461 |
0.452 |
\[
p_i(\ell_i) = \begin{cases}
\frac{100}{100 + \ell_i} & \text{ if } \ell_i \geq 100 \\
\frac{|\ell_i|}{100 + |\ell_i|} & \text{ if } \ell_i \leq -100
\end{cases} \,.
\]
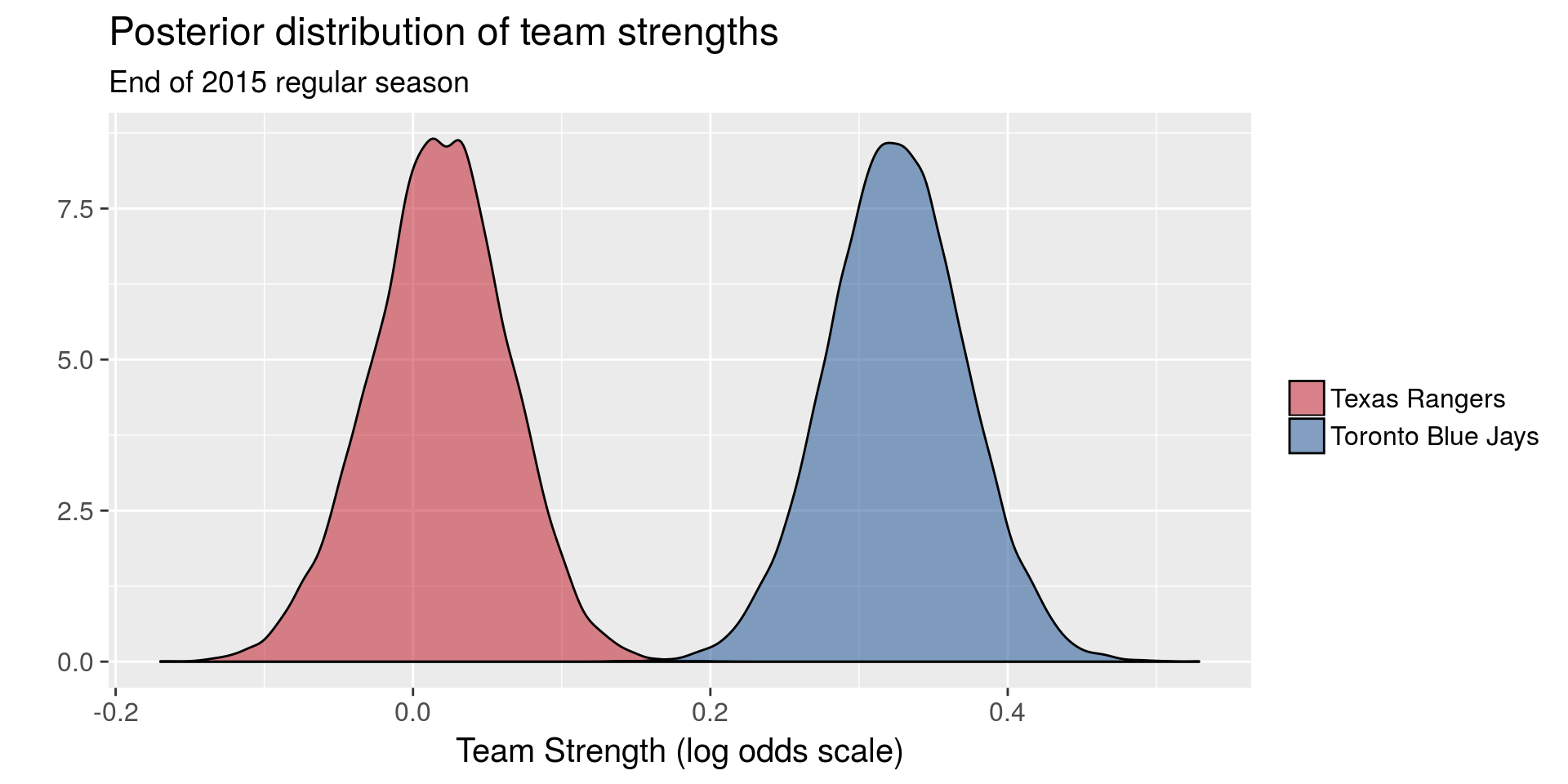
The model: definitions
- \(p_{(q,s,k)ij} =\) probability that team \(i\) will beat team \(j\) in season \(s\) during week \(k\) of sports league \(q\), for \(q \in \{MLB, NBA, NFL, NHL\}\).
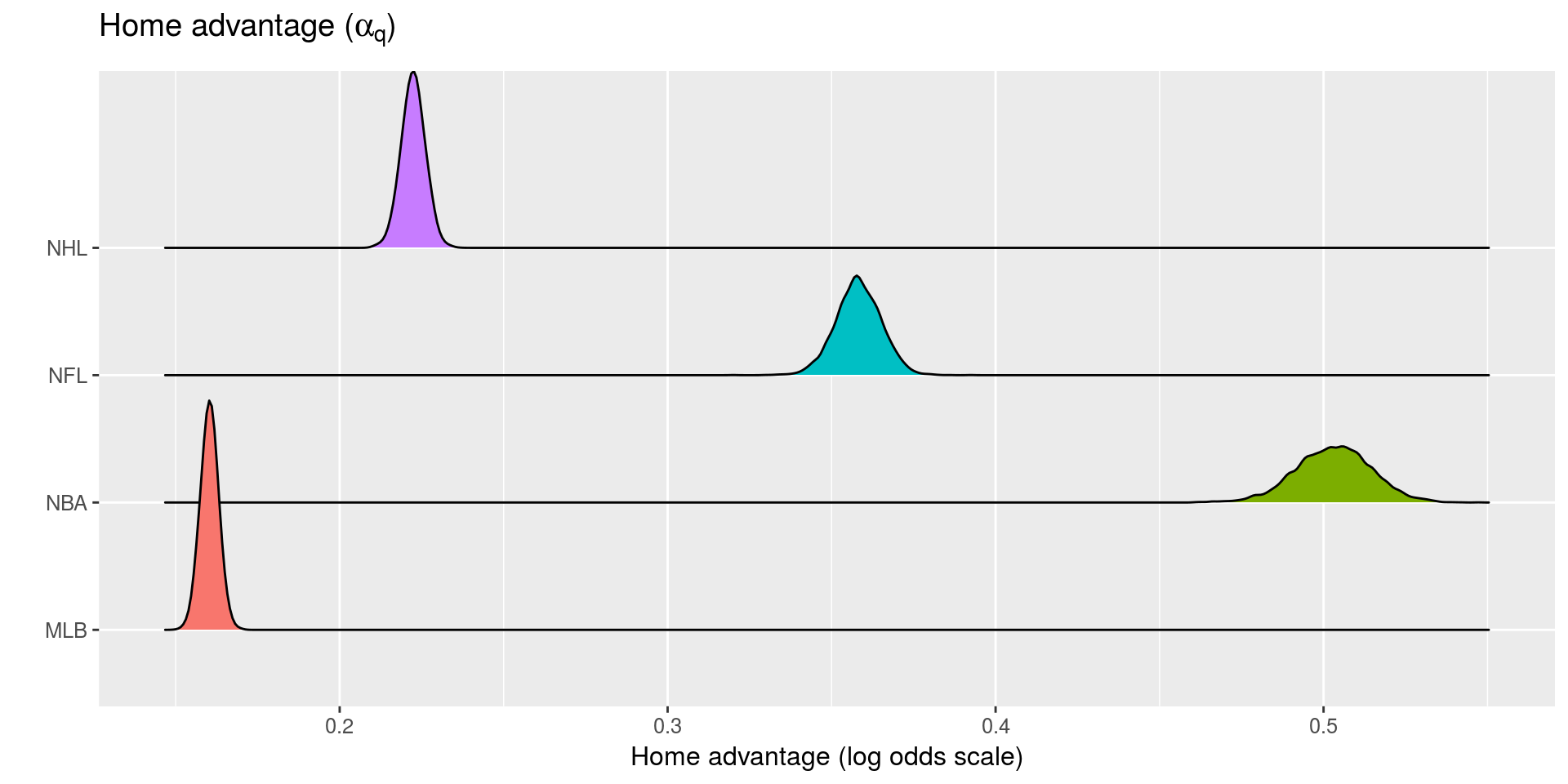
- \(\alpha_{q_{0}}\) be the league-wide home advantage (HA) in \(q\)
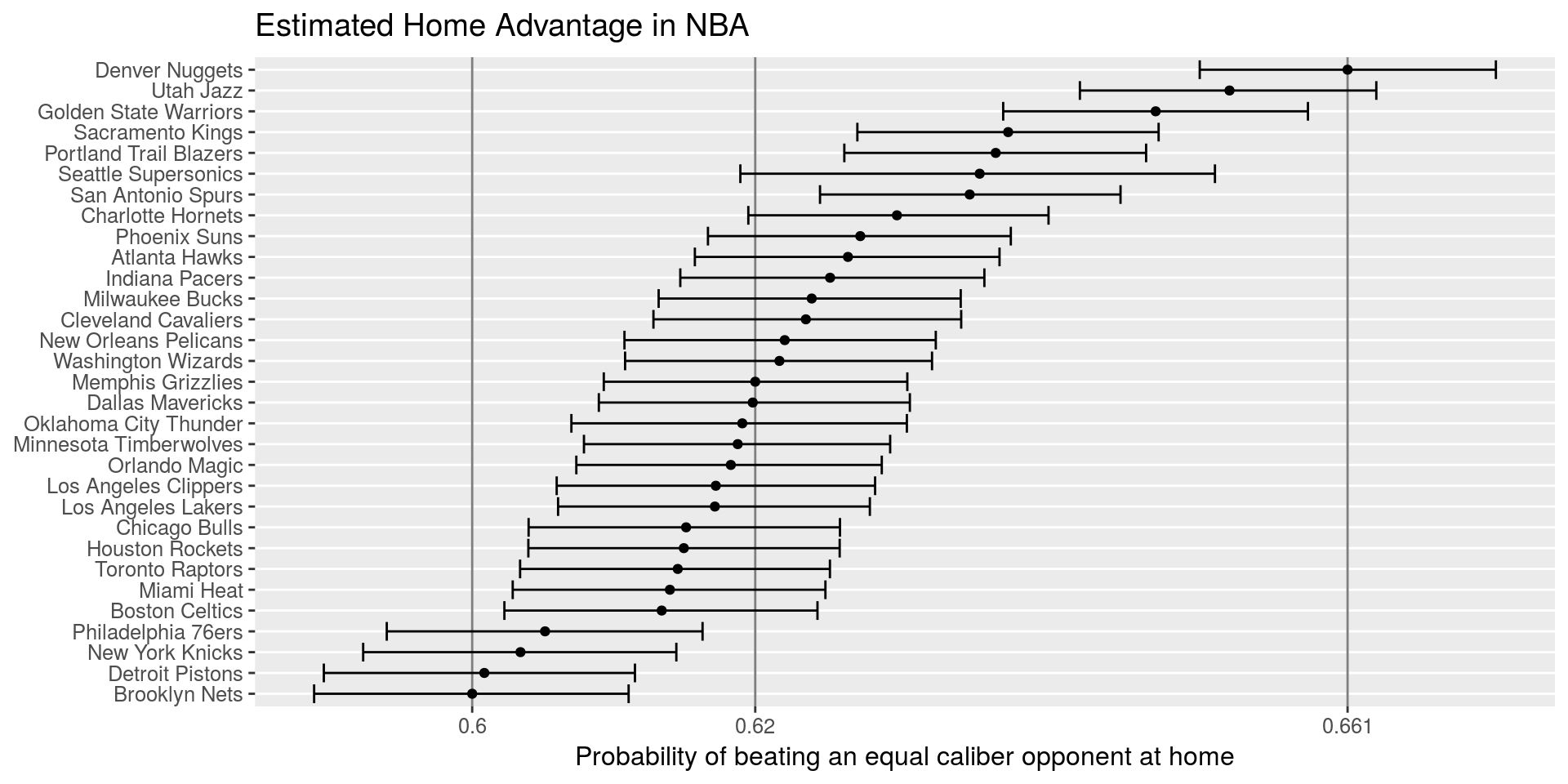
- \(\alpha_{(q) i^{\star}}\) be the extra effect (+ or -) for team \(i\) when playing at home
- \(\theta_{(q,s,k) i}\) and \(\theta_{(q, s, k) j}\) be season-week team strength parameters
The model & assumptions
\[ E[\text{logit}(p_{(q,s,k) ij})] = \theta_{(q,s,k) i} - \theta_{(q, s, k) j} + \alpha_{q_0} + \alpha_{(q) i^{\star}} \]
Assumptions:
- \(\sum_{i=1}^{t_{q}} \theta_{(q,s,k)i} = 0\)
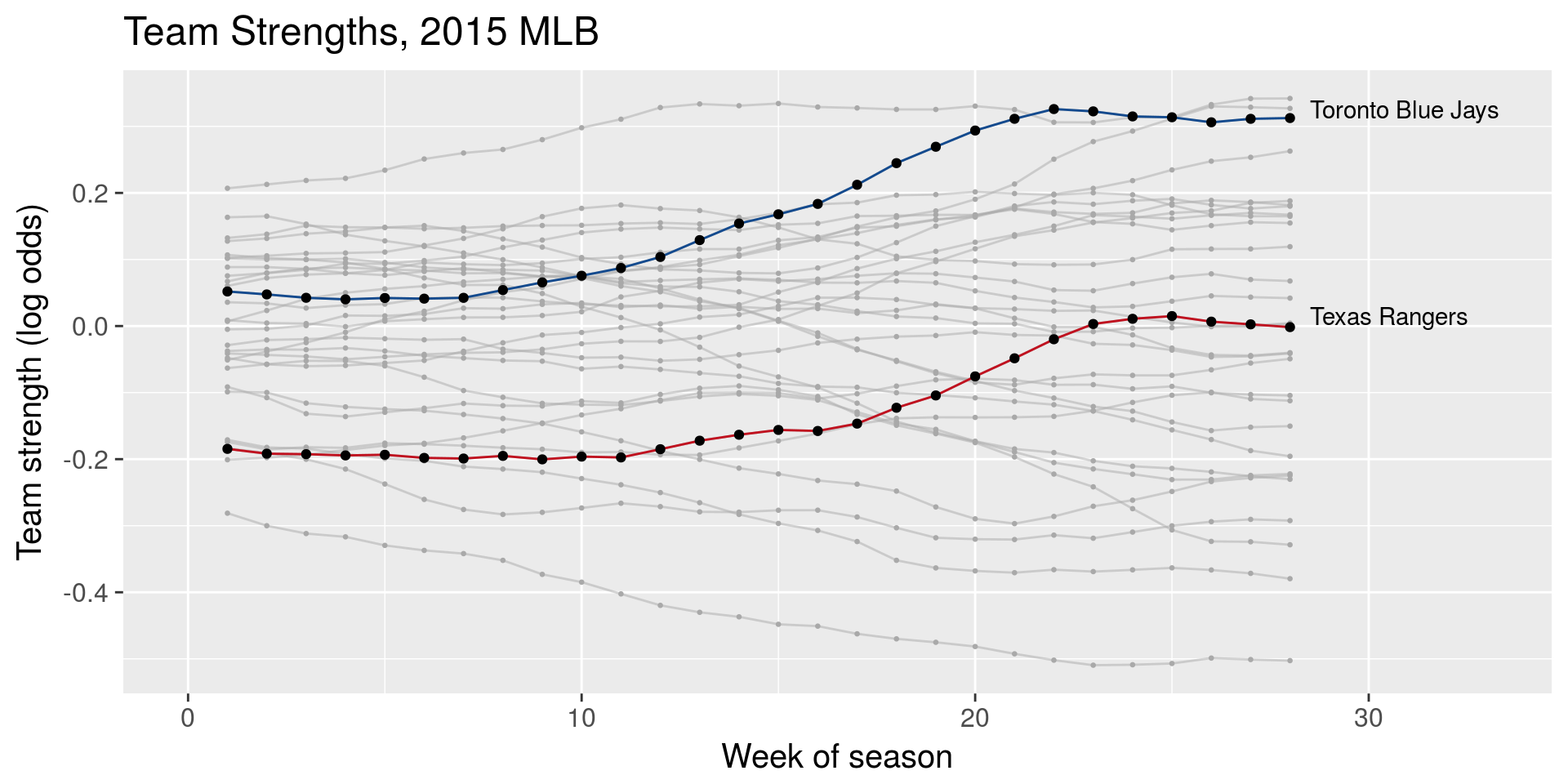
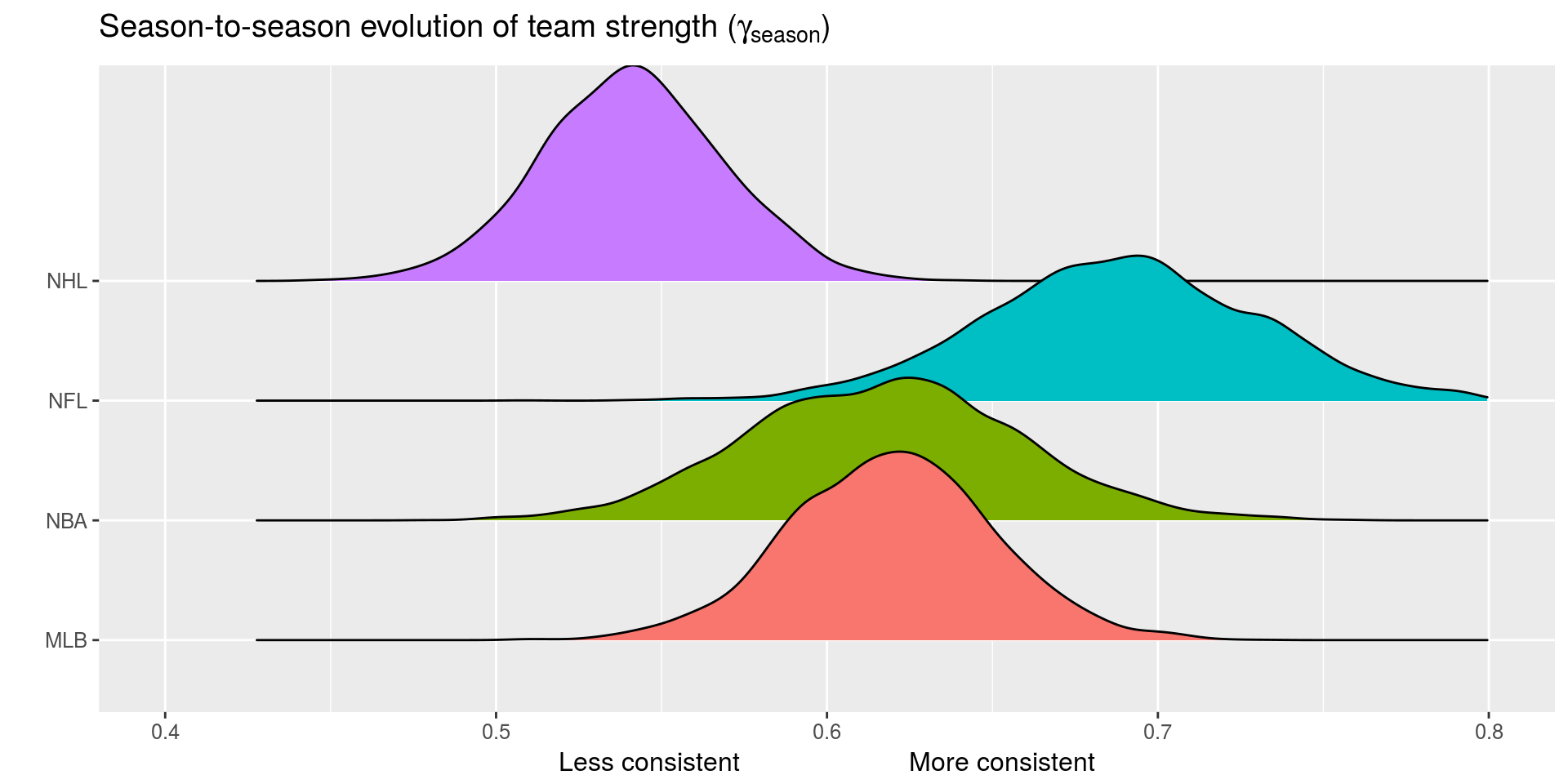
- \(E[\theta_{(i,q,s+1,1)}] = \gamma_{q, season} \theta_{(i, q,s,k)}\)
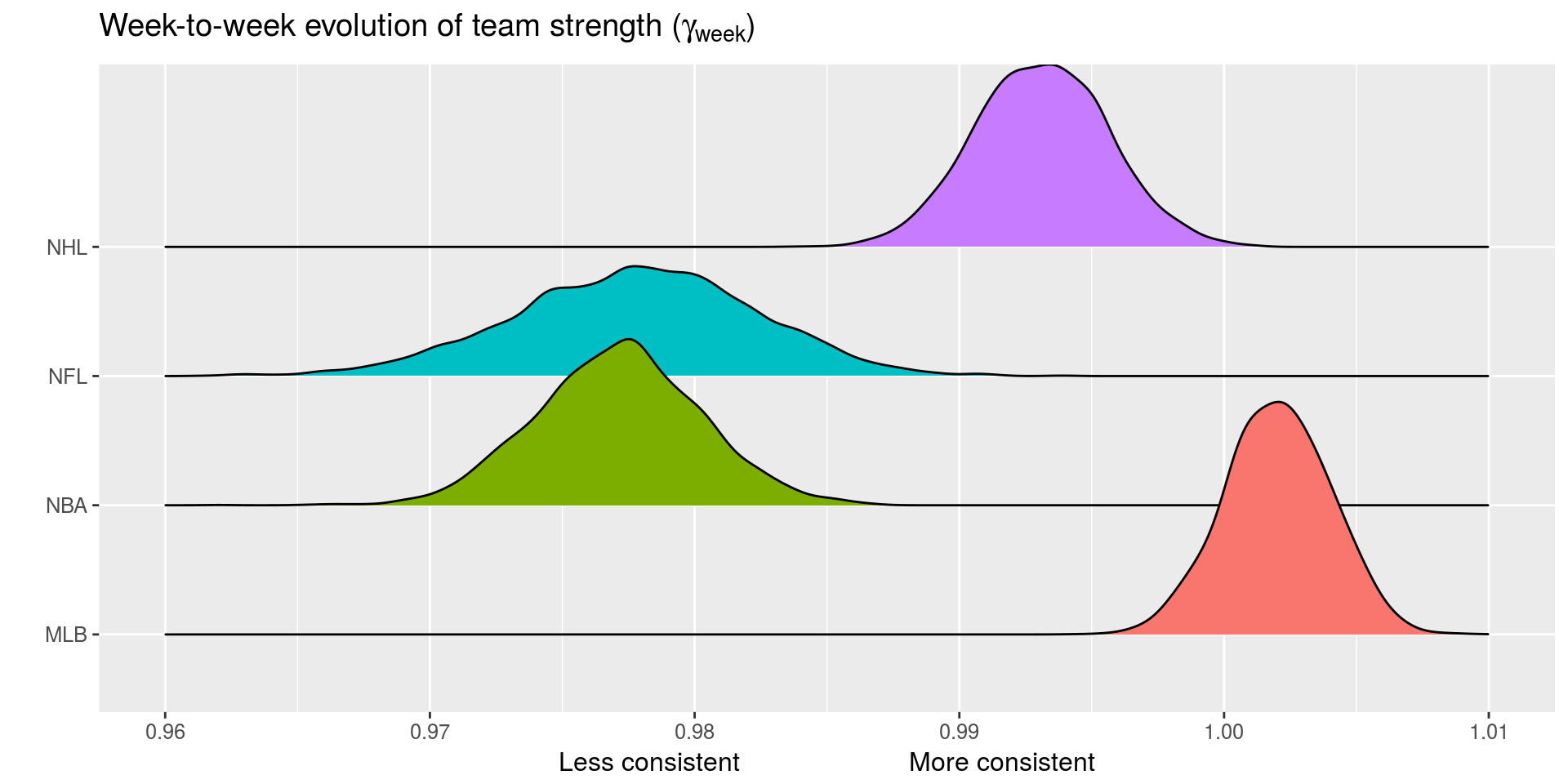
- \(E[\theta_{(i,q,s,k+1)}] = \gamma_{q, week} \theta_{(i, q,s,k)}\)
- \(\gamma_{q,week}\) and \(\gamma_{q,season}\) week/season level autogressive parameters
Fitting a cross-sport model
- Data
- 2006–2016 reg. season in MLB, NBA, NFL, NHL (Sports Insights)
- Priors
- Uniform (variance parameters) and Normal (team strength parameters)
- Software
rjags package in R statistical software
- Draws
- 20k iterations, 2k burn in, thin of 5
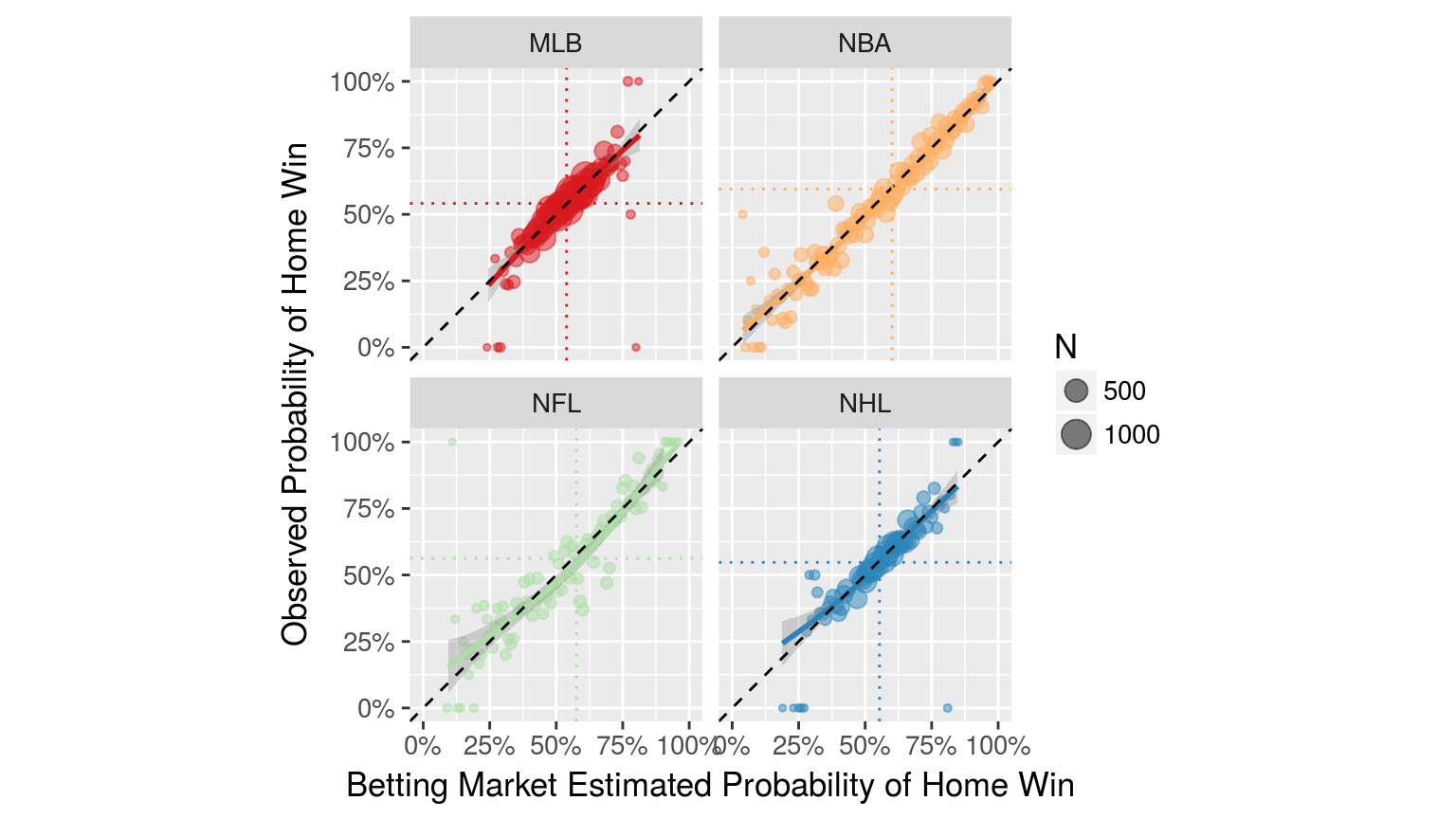
Unpredictability at a fixed point in time
How often does the best team win?
GMs need to predict the future

- Our team strengths are better at predicting future W-L
- Buyers or sellers at trade deadline?
GMs need to strategize
- Patriots rest starters in 2015 against Dolphins
- Home advantage matters in 🏈 and 🏀

GMs need a longe-term plan
“They have to rethink their whole philosophy”
Mike Milbury on the 2016 Washington Capitals losing to Pittsburgh
- There’s an immense amount of luck involved in hockey. Rethinking your philosophy on a postseason series is ludicrous
Acknowledgements: Greg

Parity in sports
More info:
Summary:
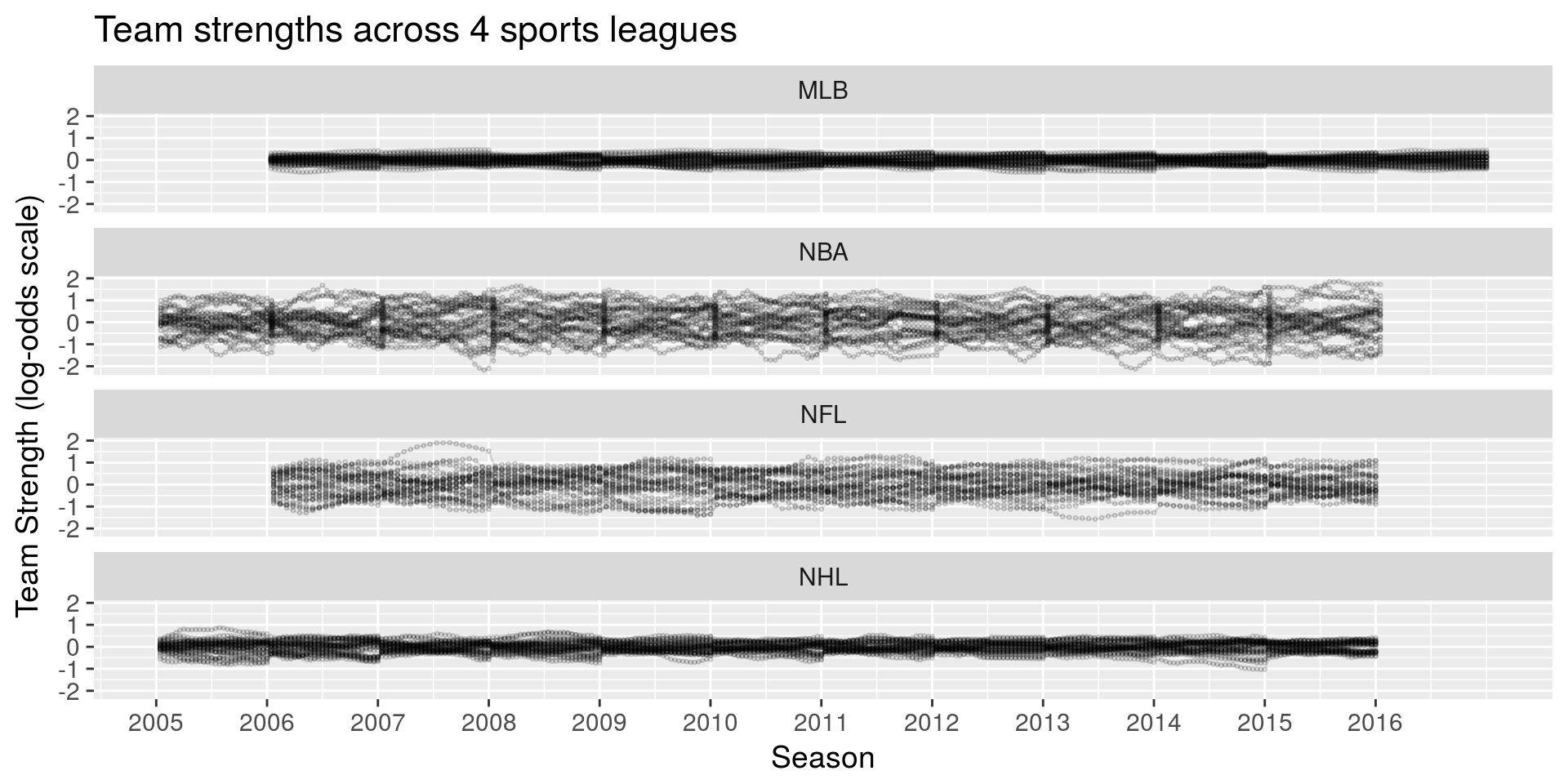
- Unpredictability at a fixed time: 🏆 (NHL), ⚾️
- Within season unpredictability 🏈
- Between season unpredictability 🏆 (NHL)
- Largest home advantage 🏀